Geometry and Integrable Systems Day
Workshop on Thursday, 11 July 2019

Speakers
Mike Eastwood (University of Adelaide)
Milena Radnovic (University of Sydney)
Mehdi Tavakol (University of Melbourne)
Andreas Vollmer (University of New South Wales)
Glen Wheeler (University of Wollongong)
Program
- 9:45-10:40 Mike Eastwood (University of Adelaide)
- Modular forms, projective structures, and the four squares theorem
- In 1770 Lagrange proved that every natural number can be written as the sum of four squares. In 1834 Jacobi gave a proof using modular forms (even though modular forms had not yet been invented). I'll explain how this works from a geometrical point of view. In fact, there are many explanations but this particular one is joint work with Benjamin Moore.
- 10:45-11:40 Mehdi Tavakol (University of Melbourne)
- Tautological classes with twisted coefficients
- For a natural number g > 1 the moduli space Mg classifies smooth projective curves of genus g. In 1969 Deligne and Mumford proved that this space is irreducible and studied some of its fundamental properties. The geometry of these moduli spaces have been studied extensively since then by people from different perspectives. Many questions about the geometry of moduli of curves involve the so called tautological classes. In this talk I will present a recent joint work with Dan Petersen and Qizheng Yin on tautological classes with twisted coefficients.
- 11:40-12:05 Morning Tea
- 12:05-1:00 Glen Wheeler (University of Wollongong)
- New results and open problems for the Willmore and related flows
- In this talk I will survey the fundamental works of Kuwert-Schaetzle, with a focus on the main unsolved issue for the Willmore flow: understanding finite-time singularities. In doing this we will skirt around the Willmore conjecture and briefly visit two or three closely related flows: the locally constrained Willmore flow, the surface diffusion flow, and Chen's flow. The talk will finish with a look at some minor new results (joint with Valentina Wheeler) that study the Willmore flow in Riemannian manifolds (with bounded geometry).
- 1:00-2:35 Lunch
- 2:35-3:30 Andreas Vollmer (University of New South Wales)
- The classification of superintegrable (Hamiltonian) systems
- Second order superintegrable systems are to date classified for conformally flat geometries in dimension 2 and 3. However, the methods do not carry over to higher dimension, as the underlying system of partial differential equations quickly grows and becomes tedious to handle. A new, algebraic-geometric approach has recently been suggested by Kress & Schoebel (2019), and was successfully applied to (non-degenerate) second order superintegrable systems on 2-dimensional Euclidean geometry. Generalizing this approach, the talk will present ongoing research aiming to extend the classification of superintegrable systems to arbitrary dimension. This is a joint project with Jonathan Kress (UNSW) and Konrad Schoebel (Weimar).
- 3:30-4:00 Afternoon Tea
- 4:00-4:55 Milena Radnovic (University of Sydney)
- Geometry of integrable billiards
- In this talk, we will use algebro-geometric aspects of billiards within quadrics in order to give analysis of their periodic trajectories.
Attendees
The speakers and organisers will be attending a lunch at The Grandstand, if you would like to join please RSVP with Dr Emma Carberry so that bookings can be arranged.
Organisers: Dr Emma Carberry & Dr Leo Tzou
School of Mathematics and Statistics, University of Sydney
Phone: +61 2 9351 3796
Email: emma.carberry@sydney.edu.au
School of Mathematics and Statistics, University of Sydney
Phone: +61 2 9351 3114
Email: leo.tzou@sydney.edu.au
Sponsors: The University of Sydney
Location
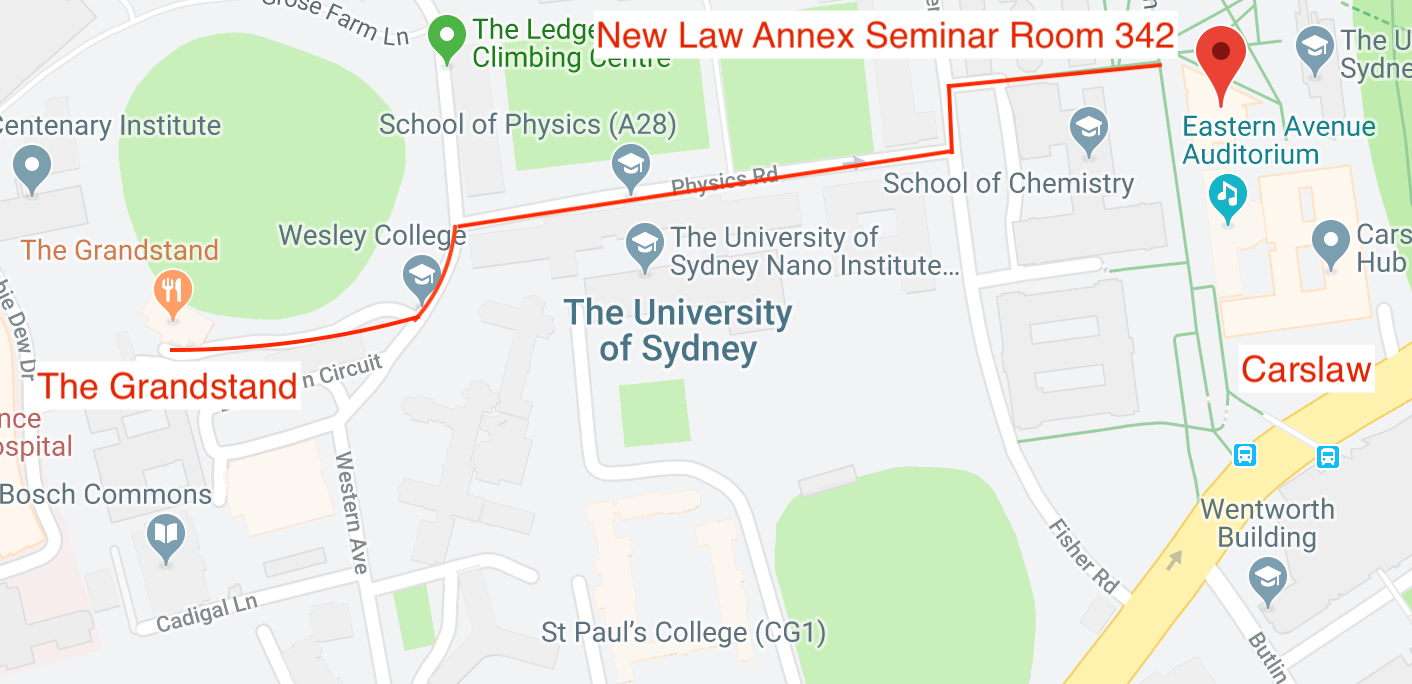
All talks will be held in the New Law Annex Seminar Room 342 and lunch will be at The Grandstand. Indicated on the campus map below.