 |
||||||||||||||||||||||||||||||||||||
|
2. Representations of vectors
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Given points A and B, we may think of the position vector
v =
The vector v is a free vector because although it has a definite direction and length it does not have any particular position in space. When using vectors to model physical phenomena it is not always appropriate to use free vectors. For example, in order to completely describe the effect of a force we need to give a vector representing the magnitude and direction of the force as well as a point of application of the force. Once we have chosen a suitable point as origin we can describe the point of application by the position vector of the point relative to the origin. It is usual to think of the vector representing the force as being confined to a line and for this reason it is often called a line vector. Two line vectors are equal if they have the same direction and length and lie along the same line. |
|||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
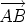 as the vector that
as the vector that 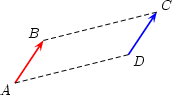 If the line segments
If the line segments  and
and 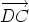 are equal; we write
this as
are equal; we write
this as 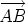
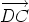 .
.