 |
||||||||||||||||||||||||||||||||||||
|
4. Multiplication of a vector by a scalar
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Using a head-to-tail procedure, a vector v can be added to itself to give the vector v + v. 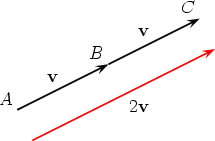
We have v = 
For example, -3v has three times the magnitude of v but points in the opposite
direction; 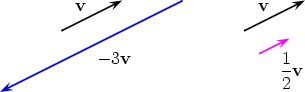
Note that -1v has the same magnitude as v but has the opposite direction, and so is the same vector as the negative of v, that is, -1v = -v.
|
|||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
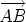 and
and 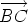 . It’s natural to write
. It’s natural to write 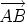
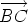
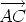 as
as 
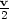 ) has magnitude
) has magnitude 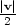 and has the same direction as
and has the same direction as