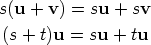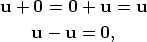|
|  |
 |
Vector algebra in geometric form
| Page 1 of 2 |
We discuss properties of the two operations,
addition of vectors and multiplication of a vector by a scalar. We do this first for free
vectors.
-
Equality of Vectors
- Two vectors u and v are equal if they have the same
magnitude (length) and direction.
-
The Negative of a Vector
- The negative of the vector u is written -u, and
has the same magnitude but opposite direction to u. If u =
 , then
-u = , then
-u =  . .
-
Commutative Law of Addition
-
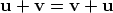
for all vectors v and u.
-
Associative Laws
-
for all vectors u, v and w and for all scalars s and t.
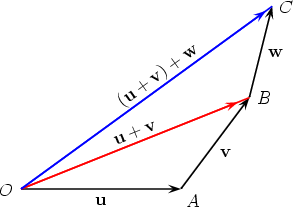
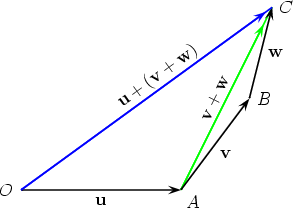
As an illustration of the first of these associative laws, we translate the three
vectors u, v and w so that they are drawn head to tail, and then draw
(u + v) + w in the first figure below and u + (v + w) underneath it,
demonstrating that both equal 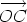 . .
We may then simply write u + v + w, without using brackets. This
associative law extends to sums of any number of vectors taken in
any order, so that the expression u1 + u2 + u3 + ...... + un is well
defined.
-
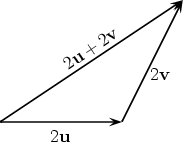
Distributive Laws
-
for all vectors v and u and for all scalars s and t.
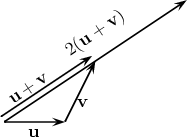
The first of these distributive laws is illustrated below in the case s = 2.
-
Laws Involving the Zero Vector
-
for all vectors u.
|

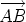 , then
, then
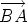 .
.
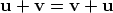
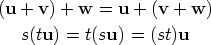
 .
.