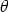The University of Sydney - School of Mathematics and Statistics

The scalar product in terms of magnitude and angles	Page 1 of 6

Suppose u and v are two non-zero vectors (in the plane or in space) with magnitudes |u| and |v|.

Translate the two vectors such that they are tail-to-tail and denote the angle between them by .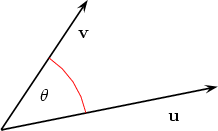

The scalar quantity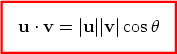

is called the scalar product (or dot product) of u and v. If one (or both) vectors are zero vectors then we define u · v = 0.

Note that it does not matter which way round the angle is measured as cos(360° - ) = cos .