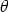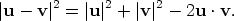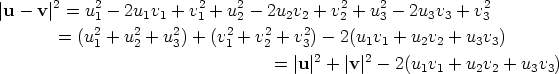|
|||||||||||||||||||||||||||||||||||||||
|
9. The scalar product
|
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
If one (or both) vectors are zero vectors then the above formula is obvious. Hence assume that u and v are non-zero. The vectors u, v and u - v then form a triangle. 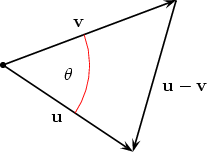
The edges of the above triangles have length |u|, |v| and |u - v|. By the law of cosines (see below) 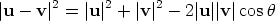
By definition u · v = |u||v| cos
By the formula for the magnitude of a vector 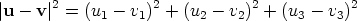 Multiplying the right hand side out we get
If we substitute the above into (1 ) we get 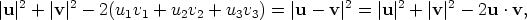 so u · v = u1v1 + u2v2 + u3v3 as claimed. Appendix: The law of cosinesThe law of cosines asserts that in an arbitrary triangle a2 = b2 + c2 - 2bc cos 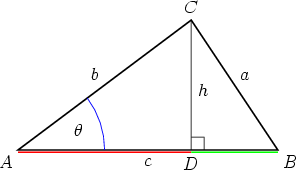
The formula follows by applying the Theorem of Pythagoras to the triangles ADC
and DBC. Note that the red line AD has length |b cos 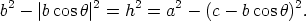 Multiplying the right hand side out we get 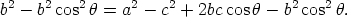
Adding b2 cos 2
|
||||||||||||||||||||||||||||||||||||||
| Feedback |
|
||||||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility