Abstract
We consider a generalised conical pendulum, where a bead is threaded on a light string of fixed length, so that it can move without friction along the string. The two ends of the string are fixed at different heights on a vertical rod and the bead undergoes uniform circular motion in a horizontal plane. Given the frequency of the motion we find the equilibrium height by using geometric properties of ellipses. We then discuss a mathematically equivalent problem that generalises to arbitrary conics.
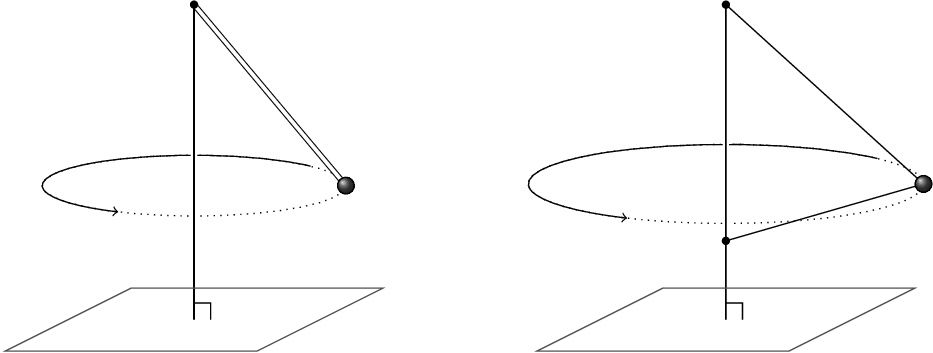
Conical pendulum and generalisation