Juncheng Wei

On some supercritical problems

We consider two types of supercritical problems. The first one is the so-called Coron’s problem: Δu + u^p = 0,u > 0 in D = Ω\B_δ(P), u = 0 on ∂D. We show that there exists resonant exponents 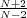< p₁ < p₂ < ... < p_j < ... such that for δ small, Coron’s problem has a solution, provided p > 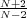and p ⁄= p_j. The second problem is nonlinear Schrodinger equation Δu - V (x)u + u^p = 0,u > 0in Rⁿ, lim_|x|→+∞u(x) = 0 We show that if V (x) = o(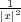), then for p > 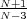, there is a continuum of positive solution. 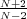If V (x) decays fast enough or V (x) is symmetric in N directions, there is also a continuum of solutions when < p ≤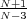.)