On the occasion of Gavin Brown’s 65th Birthday
University of Sydney, Australia, 5-6 March 2007
Qinghe Yin
Australian National Universityβ-transformations, iterated function systems, and Cantor-type sets
β-transformations and β-expansions were first introduced by Renyi (1957) and further explored by Parry (1961). Given β > 1, the β-transformation Tβ : [0,1) → [0,1) is defined by Tβx = βx (mod 1). It possesses an absolutely continuous invariant measure and is ergodic. The β-expansion of x
[0,1) is determined by Tβ. This introduces a symbolic dynamical system Σβ
with one-sided shift map. An iterated function system (IFS) is an (n + 1)-tuple (X;f0,…,fn-1), where X is a
compact metric space and each fi is a contractive map. The theory of IFS’s was first explored by
Hutchinson (1981). Many important fractals such as the Sierpinski triangle and the Cantor middle-third
set appear as attractors of certain IFS’s. We define the β-attractor Eβ for an IFS as a compact
subset, determined by Σβ, of the attractor of the IFS. In the case that all fi are similitudes with
contractive ratio 0 < r < 1 and with a disjoint condition, the Hausdorff dimension of Eβ is given
by
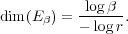
As an application of this result, we compute the Hausdorff dimension for Cantor-type sets constructed from β-expansions with β > 2. This is a joint work with John Hutchinson.