On the occasion of Gavin Brown’s 65th Birthday
University of Sydney, Australia, 5-6 March 2007
Ian Doust
University of New South WalesBalanced matrices and functions
There is an interesting family of norms on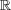 n given by
n given by
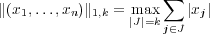
where the maximum is taken over all k element subsets of {1,…,n}. Let A be an n×n matrix with rows r1,…,rn and columns c1,…cn. We say that A is k-balanced if ∥ri∥1,k = R for all i and ∥cj∥1,k = C for all j. A little experimentation shows that R and C can be different. (The first interesting case occurs with n = 4 and k = 3.) Finding the optimal inequalities relating R and C has proven to be a challenge and there are still many open problems. The concept of a balanced function is defined analogously, now integrating of sets of a fixed measure. Our state of knowledge here is much more limited, especially if one restricts one’s attention to continuous functions. The big open question is whether a continuous balanced function on [0,1] × [0,1] exists which has a nontrivial ratio R∕C? This is joint hobby mathematics with Richard Aron (Kent State) and Nigel Kalton (Columbia, Missouri).