Research Interests
Hamiltonian dynamical systems is a modern subject with very old roots. It is located on the intersection between Mathematics and Physics. It is of fundamental importance in modelling natural phenomena, which also explains its paramount histroical role. The following list gives a brief description of my research interests. A list of possible PhD projects is also available.
Topology of Integrable Systems
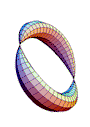 An integrable Hamiltonian System defines a singular foliation. The regular fibres of this foliation are tori.
The objective of this research is to understand the geometry and topology of this foliation and in particular
its singular fibres. The singular fibres can for example be pinched tori, as illustrated in the figure.
This torus has two pinches, corresponding to two equilibrium points of focus-focus type joined by a heteroclinic connection.
In the neighborhood of a pinched torus the regular torus bundle is non-trivial, it has monodromy.
This has been found in many examples [27,32,36].
Quantisation of these system in the semiclassical limit gives lattices of eigenstates that do not posses a global basis,
and hence no global quantum numbers, see below. The computation of the image of the energy-momentum
map with all its singularities gives the complete classification of all possible types of motion
of an integrable system. It does not, however, contain information about the dynamics on the
invariant tori; for this it has to be supplemented by the frequency map:
An integrable Hamiltonian System defines a singular foliation. The regular fibres of this foliation are tori.
The objective of this research is to understand the geometry and topology of this foliation and in particular
its singular fibres. The singular fibres can for example be pinched tori, as illustrated in the figure.
This torus has two pinches, corresponding to two equilibrium points of focus-focus type joined by a heteroclinic connection.
In the neighborhood of a pinched torus the regular torus bundle is non-trivial, it has monodromy.
This has been found in many examples [27,32,36].
Quantisation of these system in the semiclassical limit gives lattices of eigenstates that do not posses a global basis,
and hence no global quantum numbers, see below. The computation of the image of the energy-momentum
map with all its singularities gives the complete classification of all possible types of motion
of an integrable system. It does not, however, contain information about the dynamics on the
invariant tori; for this it has to be supplemented by the frequency map:
Singularities of Frequency Maps
 In KAM theory two conditions guarantee the persistence of invariant tori
under perturbations: A Diophantine condition on the frequencies and
a nondegeneracy condition ensuring that the frequency map is regular.
If the latter condition is violated we have vanishing twist. If this
occurs at a fixed point we can think of this as vanishing anharmonicity
of a non-linear oscillator. Vanishing twist can lead to instability
and unusual bifurcations. In [20] we have shown that vanishing twist
at the origin is generic in one parameter families of Hamiltonian systems
with two degrees of freedom. The goal of this research is to understand the
dynamical implications of singularities of frequency maps in Hamiltonian systems in general.
In [35] we show that near focus-focus points the
twist always vanishes. This applies in particular to the Hamiltonian-Hopf Bifurcation
[40]. And even in the basic saddle-centre bifurcation
of periodic orbits there is vanishing twist [43].
In KAM theory two conditions guarantee the persistence of invariant tori
under perturbations: A Diophantine condition on the frequencies and
a nondegeneracy condition ensuring that the frequency map is regular.
If the latter condition is violated we have vanishing twist. If this
occurs at a fixed point we can think of this as vanishing anharmonicity
of a non-linear oscillator. Vanishing twist can lead to instability
and unusual bifurcations. In [20] we have shown that vanishing twist
at the origin is generic in one parameter families of Hamiltonian systems
with two degrees of freedom. The goal of this research is to understand the
dynamical implications of singularities of frequency maps in Hamiltonian systems in general.
In [35] we show that near focus-focus points the
twist always vanishes. This applies in particular to the Hamiltonian-Hopf Bifurcation
[40]. And even in the basic saddle-centre bifurcation
of periodic orbits there is vanishing twist [43].
Dynamics of (non-) rigid bodies

 Rigid bodies are fascinating mechanical systems with many applications.
Understanding the dynamics of rigid bodies is one of the fundamental objectives
of classical mechanics, and there are still many open questions.
Since my thesis on the Kovalevskaya top I have been interested in rigid body dynamics.
Recently a levitating magnetic top was invented and in [16] we determined
its stability.
In [34] we investigate the Nekhoroshev stability of the Levitron.
The numerical integration of the Levitron is best performed using a Poisson integrator
[39].
This works for a wider class of coupled symmetric tops.
Using this integrator the long term stability near the indefinite elliptic relative equilibrium
can be investigated, which leads to the pictures on the right.
Rigid bodies are fascinating mechanical systems with many applications.
Understanding the dynamics of rigid bodies is one of the fundamental objectives
of classical mechanics, and there are still many open questions.
Since my thesis on the Kovalevskaya top I have been interested in rigid body dynamics.
Recently a levitating magnetic top was invented and in [16] we determined
its stability.
In [34] we investigate the Nekhoroshev stability of the Levitron.
The numerical integration of the Levitron is best performed using a Poisson integrator
[39].
This works for a wider class of coupled symmetric tops.
Using this integrator the long term stability near the indefinite elliptic relative equilibrium
can be investigated, which leads to the pictures on the right.
Using modern methods from geometric mechanics we are now in position to obtain a good understanding of geometric phases in the dynamics of non-rigid bodies. This can explain how, e.g., a diver can perform a twist without angular momentum around the corresponding axis, or how a cat always lands on its feet, turning in free fall. This is a new project to be expanded in the future.

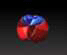

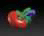 The Kovalevskaya top is one of the three integrable cases of the dynamics of
a rigid body with a fixed point. It is one of the most complicated integrable
systems with a few degrees of freedom. In my thesis I studied the action
variables of this systems. In this process we produced a movie
about the Kovalevskaya top together with the Institut für den Wissenschaftlichen Film (IWF), Göttingen.
Above on the left are some stills from it showing projections of invariant tori, the
complete movie is now available online
(german version) from the
German National Library of Science and Technology (TIB).
More information is on my web-page on the Kovalevskaya top.
The Kovalevskaya top is one of the three integrable cases of the dynamics of
a rigid body with a fixed point. It is one of the most complicated integrable
systems with a few degrees of freedom. In my thesis I studied the action
variables of this systems. In this process we produced a movie
about the Kovalevskaya top together with the Institut für den Wissenschaftlichen Film (IWF), Göttingen.
Above on the left are some stills from it showing projections of invariant tori, the
complete movie is now available online
(german version) from the
German National Library of Science and Technology (TIB).
More information is on my web-page on the Kovalevskaya top.
Quantum Monodromy
 Many fundamental models in quantum mechanics are obtained from classically
integrable systems. The quantization of integrable systems leads to the study
of the joint spectrum of commuting operators. This joint spectrum is locally
a lattice, but only recently has it been realized that globally this need not
be true. This phenomenon is called Quantum Monodromy, and it leads to the
non-existence of global quantum numbers. The underlying classical system exhibits
Hamiltonian Monodromy and its action variables are multivalued.
We have shown that Quantum Monodromy occurs in physically relevant systems
[27,30,37] and calculated their spectra.
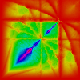
Recently we have constructed examples that allow for arbitrary monodromy matrices,
answering one of the outstanding questions in the field [44].
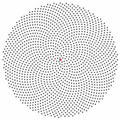
The picture on the left is a lattice with monodromy given by the cat map obtained
from this example.
Many fundamental models in quantum mechanics are obtained from classically
integrable systems. The quantization of integrable systems leads to the study
of the joint spectrum of commuting operators. This joint spectrum is locally
a lattice, but only recently has it been realized that globally this need not
be true. This phenomenon is called Quantum Monodromy, and it leads to the
non-existence of global quantum numbers. The underlying classical system exhibits
Hamiltonian Monodromy and its action variables are multivalued.
We have shown that Quantum Monodromy occurs in physically relevant systems
[27,30,37] and calculated their spectra.
Recently we have constructed examples that allow for arbitrary monodromy matrices,
answering one of the outstanding questions in the field [44].
The picture on the left is a lattice with monodromy given by the cat map obtained
from this example.
(Integrable) Water Wave Equations
The KdV equation is the most important shallow water wave model equation. It is obtained from the full Euler equations by an asymptotic expansion. Many equations have been suggested as improvements of the KdV equation. We have shown [26] that the integrable Camassa-Holm equation is a higher order shallow water wave equation, which has advantages over other models. A major tool in this work is a nonlocal normal form transformation for PDEs, which is explored systematically in [33].
Symplectic Maps and the Variational Principle
 Area preserving twist maps are probably the best understood models for
Chaos in Hamiltonian systems. Recently the variational methods of
Aubry-Mather theory have allowed for substantial progress. I have used
the variational approach for extensive numerical studies of periodic
orbits and their bifurcations [19,22]. We now investigate
the construction of symbolic dynamics not only in the ergodic case [12] but
also in the most complicated regime of coexisting regular and chaotic motion.
The use of high performance
computing and specially developed numerical methods now gives the opportunity
to obtain a complete overview of periodic orbits for one parameter families
of maps. In [25] we have done this for the family
of Limaçon billiards.
Using numerical continuation we were able to extend symbolic dynamics from
a hyperbolic limit into a regime with stable periodic orbits [41].
This lead to a conjecture about the coding of rotational elliptic orbits of the Hénon map.
Area preserving twist maps are probably the best understood models for
Chaos in Hamiltonian systems. Recently the variational methods of
Aubry-Mather theory have allowed for substantial progress. I have used
the variational approach for extensive numerical studies of periodic
orbits and their bifurcations [19,22]. We now investigate
the construction of symbolic dynamics not only in the ergodic case [12] but
also in the most complicated regime of coexisting regular and chaotic motion.
The use of high performance
computing and specially developed numerical methods now gives the opportunity
to obtain a complete overview of periodic orbits for one parameter families
of maps. In [25] we have done this for the family
of Limaçon billiards.
Using numerical continuation we were able to extend symbolic dynamics from
a hyperbolic limit into a regime with stable periodic orbits [41].
This lead to a conjecture about the coding of rotational elliptic orbits of the Hénon map.
Semiclassical Quantization
There are two reasons to supplement quantum mechanics with semiclassical methods: Efficiency in the computation of spectra and the hope to gain understanding through the classical point of view. Initially focusing on integrable quantum billiards we have shown [10] how to modify the Berry-Tabor trace formula in the presence of a separatrix, and later extended some of these results to higher dimension [17]. Currently we study a family of (non-integrable) billiards and use minimal action orbits for its quantization.
Collaborators
- Arnd Bäcker
- Alexey Bolsinov
- Richard Cushman
- Franceso Fasso
- Andrea Giacobbe
- Georg Gottwald
- Heinz Hanßmann
- Darryl Holm
- Jim Howard
- Alyosha Ivanov
- Hector Lomeli
- Vladimir Matveev
- Richard Montgomery
- Jim Meiss
- Alvaro Pelayo
- Peter Richter
- David Sterling
- Alexei Tsygvintsev
- Sasha Veselov
- Vu Ngoc San
- Holger Waalkens
- Jan Wiersig
Students
- Sean Dawson (PhD, Sydney): Relating Classical and Quantum Integrable Systems
- Diana Nguyen (PhD, Sydney): Integrable Systems Arising from Separation of Variables
- Nathan Duignan (PhD, Sydney, 2019): On the Regularisation of Simultaneous Binary Collisions
- Joachim Worthington (PhD, Sydney, 2017): Stability Theory and Hamiltonian Dynamics in the Euler Ideal Fluid Equations
- William Tong (PhD, Sydney, 2015): Coupled Rigid Body Dynamics with Application to Diving
- Danya Rose (PhD, Sydney, 2015): Geometric phase and periodic orbits of the equal-mass, planar three-body problem with vanishing angular momentum
- George Papadopoulos (MSc, Sydney, 2013): Semi-global symplectic invariants of the Euler top
- Sven Schmidt (PhD, Loughborough, 2008): Resonant Elliptic Equilibria in Hamiltonian Systems
- Chris Davison (PhD, Loughborough, 2006): Geodesic Flow on the Ellipsoid with Equal Semi-Axes

Professor of Applied Mathematics
School of Mathematics and Statistics
University of Sydney NSW 2006
Australia
holger.dullin@sydney.edu.au
Phone: +61 2 9351 4083
FAX: +61 2 9351 4534
Office: 714 Carslaw F07
Publications
Current Teaching
MATH1902 Linear Algebra (Adv.)MATH3977 Lagrangian and Hamiltonian Dynamics