Holger R. Dullin's page on the Kovalevskaya Top
During my
PhD thesis
we produced a
movie about the Kovalevskaya top
(german version),
and a
booklet
that explains the theory behind the movie.
Most of the colour pictures from my thesis are shown below,
many of them also appeared in [3]
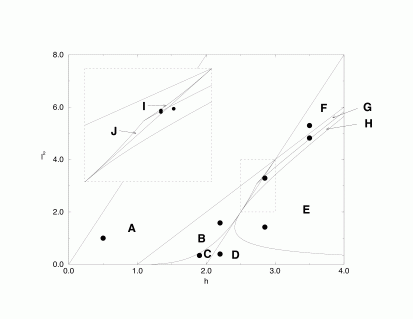
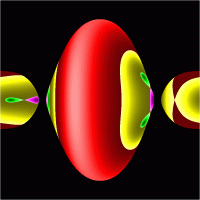
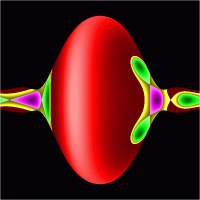
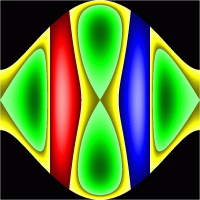
Poincare Sections
There are 10 topologically different Poincaré Sections a-j.
Same colour and same lighness gives the invariant curve obtained from
the intersection of the reduced two-torus with the surface of section.
Each hue (red, green, blue, etc.) represents a family of tori which can
be deformed into each other at fixed energy and angular momentum.
Colour jumps indicate separatrices, while the light or dark centres
are stable reduced periodic orbits.
There is an additional discrete symmetry when the angular momentum vanishes (c0, d0).
Each pictures has a particular value of energy and angular momentum.
The ten regions of different foliations of the reduced energy surface
are indicated in the phase diagram.
The disks show where the parameters
for the picture of the respective region were chosen.
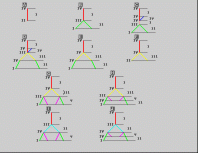
The corresponding Fomenko graphs
(with the same colour scheme)
Medium Size
a  b
b  c
c  d
d  e
e  f
f 
a-f 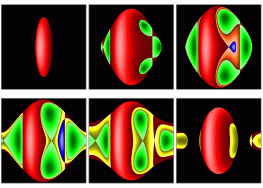
g  h
h  i
i  j
j  c0
c0  d0
d0 
g-j,c0,d0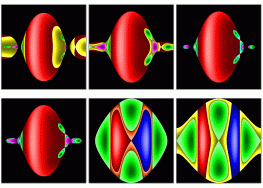
Stacks
Here all sections for fixed energy and with all possible values of the
angular momentum are stacked and then the stack is cut along the middle.
This is an attempt to visualise the full system with three degrees of
freedom by taking a section of a section.
Each 3-Torus of the full system appears as either 2 or 4 points in a stack.
The black lines indicate families of 2-tori.

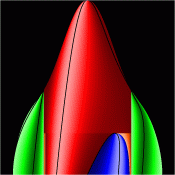
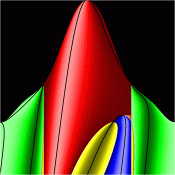
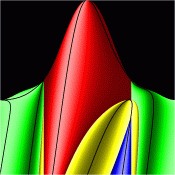
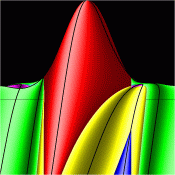
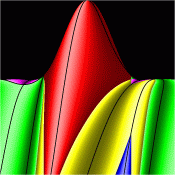
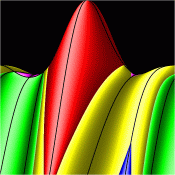
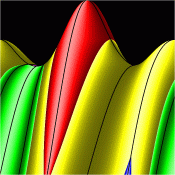

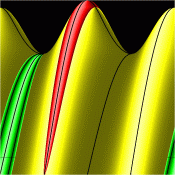
Energy Surfaces in Action Space
Without symmetry reduction, for energy 12.
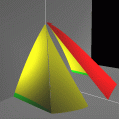
The original figures of [3] and my thesis
Figure 3 of [3], Fig 4.5 of thesis
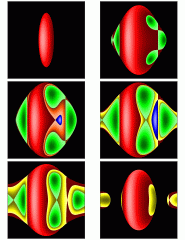
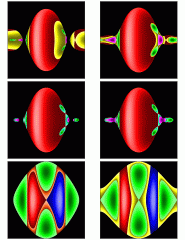
Figure 7 and 10 of [3], Fig 4.6 and 4.7 of thesis
In Fig 10 symmetry reduced energy surfaces in action space are shown for 6 different energies.


Figure 8 and 11 of [3]

Large Size




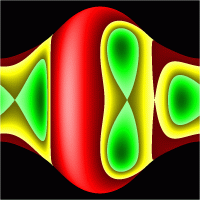




UP:
Home
| Applied Mathematics
| School of Mathematics and Statistics
| The University of Sydney
