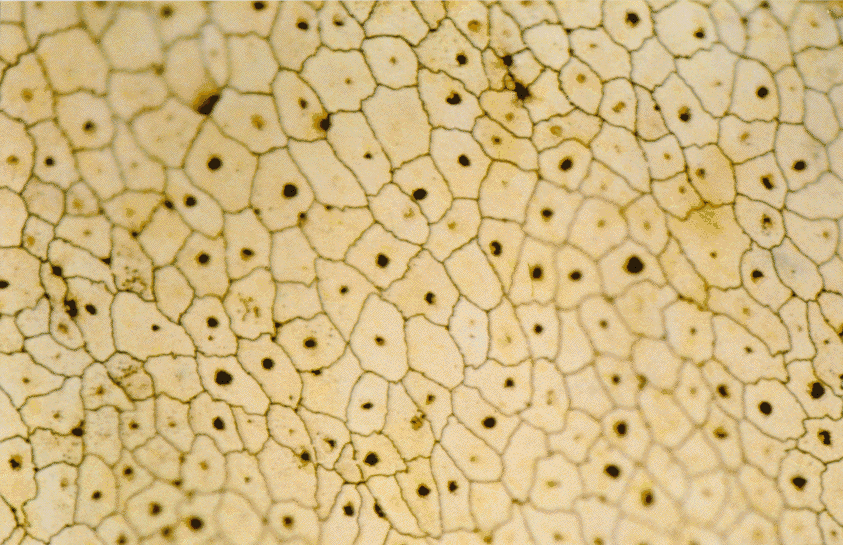
 |
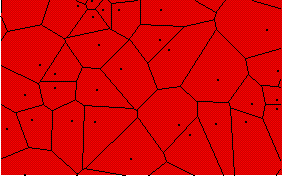
The Voronoi tessellation constructed from particles which form a Poisson process. Each polygon contains one particle and comprises the region of the plane closer to that particle than to any other. There are no edge effects in this picture, as the figure was constructed initially on a much larger domain. |
 |
|
 |
Random tessellations can be quite general in character, with vertices of all orders and polygons of all sizes and shapes. A general theory of ergodic homogeneous tessellations is developed in #10 and #14. Results include the first proofs (and correct statement) of topological linkage formulae where, for the typical polygonal cell, assumed convex, and, for the typical vertex, θ = the mean # of arms and φ = the proportion of vertices which have an angle of 180 degrees between two of its adjacent arms. Note: φ is the phi in the formula. |
 |
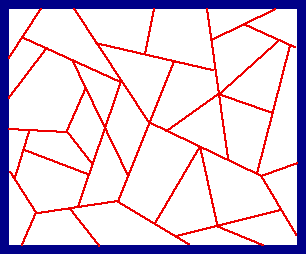
This is an example of the "falling-leaf" tessellation, studied in #58. Congruent polygonal leaves fall randomly onto the plane covering leaves which have fallen earlier. Our interest is the random tessellation formed by the leaf edges when temporal equilibrium is reached. Results are given in #58 for stochastic properties of the tessellation's polygons and vertices (even when shapes are more elaborate, with curved edges). |