Differential Geometry (MATH3405)

updates

introduction

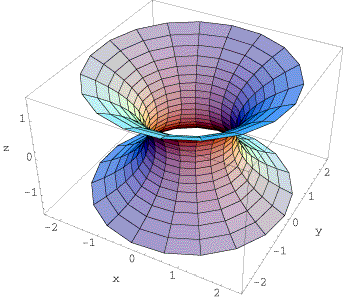
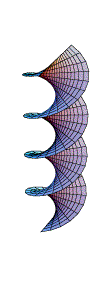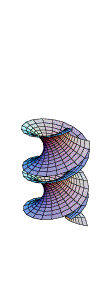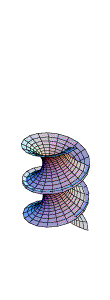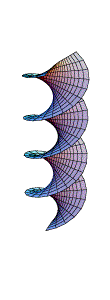
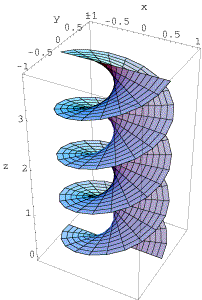
What are these surfaces and what do they have in common?

The picture on the left shows a catenoid, the surface of revolution of a catenary. There are many geometric properties that distinguish the catenoid from a hyperboloid of one sheet. One key property can be described as follows. If you imagine the boundary circles made up of wire, then the shape of the catenoid is exactly what you would see if you dipped the two circles (keeping their relative position fixed) into soap solution. The law of surface tension governing the soap film results in a surface that minimises area amongst all surfaces with boundary consisting of the two circles. Mathematically, we will characterise a minimal surface by the property that the mean curvature at every point of the surface is zero. This is an example of how a local property (mean curvature zero at each point) determines a global property (the surface minimises area). The catenoid has another fascinating property, which is illustrated by the animation: It can be deformed into a helicoid in such a way that every surface along the way is a minimal surface, which is locally isometric to the helicoid.

These pictures and the animation are due to Weiqing Gu and can be found here, along with many other delightful pictures and computations.

course description

The geometry of curves and surfaces in three dimensional space is studied using techniques from linear algebra and calculus. We will determine various geometric quantities associated to a curve or surface. An example of such a quantity is the length of the acceleration vector at a point of a curve in R³ (where the curve is parameterised by unit speed). This length is the curvature of the curve at that point. We will show that a non-contant curve with curvature zero at every point must be a line. This is another key example of how local behavior (the curvature at each point is zero) determines global behavior (the curve is a straight line).

Similar to the relationship between local and global properties, we will also compare intrinsic and extrinsic properties of curves and surfaces. For example, bending a sheet of paper changes its extrinsic geometry, but not its intrinsic geometry. An example of an intrinsic quantity (that is not changed by bending the sheet of paper) is the Gauss curvature, which is introduced in the last third of this course. The definition of the Gauss curvature makes essential use of the position of a surface in space. However, Gauss showed that it is nevertheless independent of the position in space and only depends on the geometry of the surface. He was so pleased with this result that he called it "Theorema Egregium," a remarkable theorem.

Another concept introduced in this course is the topology, or shape, of a geometrical object. Two surfaces have the same topology if you can deform one into another by bending, twisting, stretching and deforming, but not tearing it. Two spheres of different radii certainly have the same topology, but we will see that they are distinguished by their curvatures. The same is true for any sphere and a (non-trivial) ellipsoid. Towards the end of the course, we will come across two amazing results: A theorem of Poincare (relating the indices of a vector field at certain points of a closed surface to the topology of the surface), and the Gauss-Bonnet Theorem (relating the total curvature of a closed surface to the topology of the surface).

outline

I will follow "Differential Geometry of Curves and Surfaces" by Manfredo do Carmo; covering a little less than half of the material in the text. One copy of the text will be on reserve in the Dorothy Hill Physical Sciences & Engineering Library in Hawken (50), along with other references. Below is a tentative outline for the course:

As there are 13 weeks in the semester, the above outline leaves room to digress, elaborate, recall assumed background material, and to prepare for the transition from a surface in 3-dimensional Euclidean space to the concept of an abstract 2-dimensional Riemannian manifold.

background

The prerequisite for this course is MATH2000, and I will assume knowledge of the concepts and methods introduced there (and in its prerequisites MATH1051 and MATH1052). There are two recommended prerequisites, MATH2400 and MATH2301. They are recommended not so much for contents, but rather for general mathematical training. If not all students have taken MATH2400, I will introduce the Inverse Function Theorem in the context of 1.5, and the Implicit Function Theorem in the context of 2.3. If not all students have taken MATH2301, I will be a bit more gentle with algebraic notions such as tangent spaces, differential forms and the shape operator.

If you wish to revise the background material, it should suffice to go over the notes, homework, assignments and exams of the prerequisite. If you feel enthusiastic, an excellent way of revising and deepening this material would be to work through Michael Spivak's "Calculus on Manifolds," which starts with the inner product on Rⁿ and ends with Green's Theorem and the Divergence Theorem.

links

mathematica

Mathematica notebooks are linked to many of the minimal surfaces below. If you have access to Mathematica, they are certainly fun to play with. Once we have done enough calculations by hand, I will use Mathematica from time to time in order to illustrate the material of the course.

lectures

tutorial

consultation hours

assessment (overview)

assessment (assignments)

Each assignments will be given out during the lecture a week before its due date, and it will be made available on this web-page after that lecture. Late assignments will receive no marks and only be marked for feedback. Students who are unable to submit an assignment and qualify for special consideration should contact me.

Each assignment is worth 4% of the final mark, and needs to be returned by the due date to the assignment box for this course.

The solutions are posted on blackboard.

assessment (mid-semester test)

The mid-semester test will cover all material up to the test. It is a 45 minute closed book exam which will be held during the normal lecture time. No calculators are permitted in this mid-semester test.

assessment (final exam)

The final exam is worth 50% of the final mark and covers material from the entire course. It will contain a list of formulas without context or hypotheses. You can have a look at the current version. The only changes in later versions will be: corrections and additions; nothing will be taken off.

Wednesday, 9 November, at 11:15 in 24-S603

(10 min perusal; 120 min duration)

The exam may include the following:

1) explicit, computational questions

2) ask you to state theorems/definitions

3) applications of major theorems

4) questions that require insight

5) proofs or examples from the lectures or assignments

As to 5): If I ask you to prove something, it should be straight forward. For long or involved proofs in the lecture notes, I don't expect you to know all the details, but rather to know the storyline. I might ask you "Why is Gaussian curvature intrinsic?" or "What is the relationship between FFF and SFF?", and as a response, I would only expect you to say two or three vague sentences that highlight the key ideas.

What is almost certain to be on the exam:

6) An application of the General Gauss-Bonnet Theorem

7) A question about a smooth real-valued function on some surface that requires the concept of the critical points of the function (including the Hessian or vector fields).

textbook

My lectures will be based on the following text, which is also used as the main source of exercises.

A copy of the textbook, along with all other references, will be on reserve in the Dorothy Hill Physical Sciences & Engineering Library in Hawken (50). This course will cover a little less than half of the material in the book. You can purchase the text at the Co-op bookshop, or order it at Amazon.com. The latter option appears to save you at least 50%.

A list of errata for the book by Bjorn Poonen.

suggested exercises from the book

Below list of problems matches the material we have covered in each paragraph (even though the text in the related sections may not). You are, of course, encouraged to do more problems. If you're really stuck with an exercise, have a look at the errata to see whether there are crucial typos!

§1 Curves in Rⁿ:

1.2 Exercises 2, 4

1.3 Exercises 1, 2, 10

1.4 Exercise 13

§2 Regular surfaces:

2.2 Exercises 1, 2, 3, 4, 5, 7, 10, 11, 13

2.3 Exercises 3, 4, 5, 8

§3 Tangent spaces and fundamental forms:

2.4 Exercises 1, 2, 3, 8, 16

2.5 Exercises 1, 3, 7, 10

2.6 Exercises 1, 2, 7

3.3 Exercises 1, 5a, 5b, 6, 18

4.2 Exercises 1, 9, 10, 11, 12

4.3 Exercises 1, 2, (3 is on A5), 4, 9

4.6 Exercise 5

§4 Geodesics:

4.4 Exercises 7, 17

4.7 Exercise 4

§5 Integration on surfaces:

2.5 Exercises 5, 11

2.6 Exercise 3

4.2 Exercise 19

4.5 Exercises 1, 2, 4

§6 Hessians, vector fields and Gaussian curvature:

3.3 Exercises 22(a), 23(a)

3.4 Exercises 1, 2, 4

4.5 Exercises 6, 7, 8

[Hopf] Exercise after 1.6

suggested reading related to what was covered

Below list of readings matches the material from do Carmo's book that we have covered. Parts of this should be viewed as revision. Some sections were not covered entirely, and some gaps will be filled in week 13. The material from Chapter 3 was done quite differently (especially the discussion of geodesics). A good reference for this (and other material) is the section on Surfaces in R³ in the notes on Geometry of Surfaces by Nigel Hitchin. You should also read the handout about the Poincaré-Hopf Index Theorem.

Background material:

1.4; Appendix to Chapter 2

Curves in Rⁿ:

1.2, 1.3, 1.5

Surfaces in R³:

2.2, 2.3, 2.4, 2.5, 2.6, 3.3, 4.2, 4.5

materials

references

Below books by Berger and Spivak are encyclopedic. Both contain a wealth of interesting facts, material that is hard to find elsewhere, historical accounts and lots of pictures. They are truly meant as references, and not as essential reading.

bed-time reading

These two books give nice, informal introductions, heuristic arguments and contain excellent illustrations. They are really enjoyable to read.

help and advice