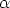Engineering examples for The projection of a vector

Example 1

Consider a block on a plane inclined from the horizontal by the angle .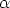

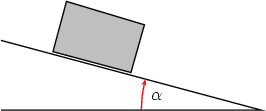
The magnitude of the friction force F acting on the block is assumed to satisfy

|F |< m |N |,

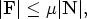
(1)

where is the coefficient of friction and N the force acting normal to the plane. Determine the angle of critical equilibrium, that is, the maximal angle at which the block will stay still.

Solution

The forces acting are the gravitational force G, the friction force F and the normal force N.

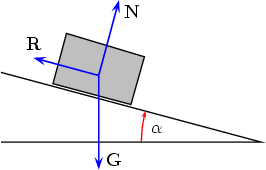
For the block to stay still the total force must be zero:

F + G + N = 0.

Now choose a coordinate system such that the x-axis is parallel to the inclined plane and the y-axis is pointing upwards.

Writing R = F_xi, N = N_yj and G = G_xi + G_yj we get

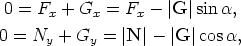0 = Fx + Gx = Fx- |G |sin a, 0 = N + G = |N |- |G |cosa, y y

or equivalently

Dividing the two equations we obtain

Fx sin a |N-|= cosa-= tana.

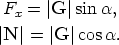Using (1 ) we deduce that

m|N | F m = ----- > --x-= tana. |N | |N |

Hence the block stands still if and only if > tan 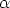, so the critical angle is 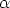= tan ^-1.