Close

Examples for Lines in space

Example 1

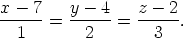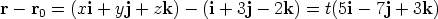
Find a parametric vector equation and Cartesian equations of the line through (1, 3,-2) parallel to 5i - 7j + 3k.

Top of page

Solution

According to our assumptions r0 = i + 3j - 2k is a position vector of a point on the line. Hence the parametric vector equation of the line is
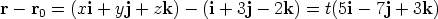
r- r0 = (xi + yj + zk) - (i + 3j - 2k) = t(5i- 7j + 3k)

or equivalently

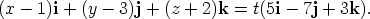
(x - 1)i + (y - 3)j + (z + 2)k = t(5i - 7j + 3k).

The parametric equations are then

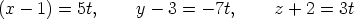
(x- 1) = 5t, y - 3 = - 7t, z + 2 = 3t

so the Cartesian equations are

x- 1 y - 3 z + 2 ------= ------= -----. 5 - 7 3

Example 2

Find the parametric vector equation, and the cartesian equations, of the line through A(7, 4, 2) and B(8, 6, 5).

Top of page

Solution

The required line passes through the point A(7, 4, 2) and is parallel to the vector
-AB--> = (8- 7)i + (6 - 4)j + (5 - 2)k = i + 2j + 3k.

Its parametric vector equation is therefore

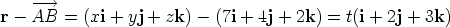
---> r- AB = (xi + yj + zk) - (7i + 4j + 2k) = t(i + 2j + 3k)

or

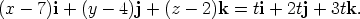
(x - 7)i + (y - 4)j + (z - 2)k = ti + 2tj + 3tk.

So the parametric equations of the line are

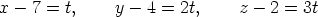
x - 7 = t, y- 4 = 2t, z - 2 = 3t

and the Cartesian equations are

x---7-= y---4-= z---2. 1 2 3