Examples for Planes in space

Example 1

Find the vector and cartesian equations of the plane through (1, 3,-2) perpendicular to 5i - 7j + 3k.

Solution

and hence the vector equation of the plane is

or

Expanding the scalar product produces the cartesian equation

or

Example 2

Find a equation of the plane that passes through C(2, 1, 5) and is perpendicular to the line through A(0, 1, 1) and B(1,-1,-1).

Solution

is normal to the required plane.

The position vector of C is 2i + j + 5k.

Thus a vector equation of the plane is

or

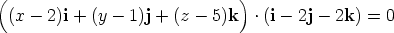
and so a Cartesian equation is

or

Example 3

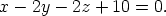
Let A(-1, 3, 1), B(2,-2, 0) and C(1, 1,-1) be three points in space.

• Give an equation for the plane through A, B and C.
• Write down an equation for the line perpendicular to the plane through A, B and C passing through A.

Solution

• The normal direction of the plane is given by the vector product of

  and

  

  The vector product of the two is

  

  It does not matter how long the vector perpendicular to the plane is. Hence we can replace 8i + 4j + 4k by n = 2i + j + k. The equation of a plane has the form ax + by + cz + d = 0, where ai + bj + ck is a vector perpendicular to the plane. Hence in our situation we can choose

  

  and so the equation of the plane is 2x + y + z + d = 0 for some d. To determine d we substitute one point on the plane into the equation; for instance A(-1, 3, 1). We then get -2 + 3 + 1 + d = 0, and so d = -2. Thus

  

  is an equation of the plane.

• We have already computed the direction, n, perpendicular to the plane. Hence the equation required is