
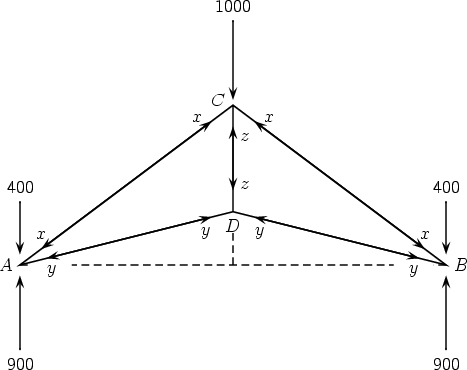
Consider a roof truss problem. The following is a drawing of a simple roof truss, consisting of five light weight bars AC, AD, BC, BD and CD, the whole structure resting on walls at A and B, which are on the same horizontal level. The structure is symmetrical about the line CD. A and B are 40 meters apart, and C, D are 15 meters, 5 meters respectively above the level of A and B. Loads of 1000kg, 400kg and 400kg rest on C, A and B respectively, causing reactive vertical forces at A and B, as shown.

Calculate the magnitudes of the reactive forces at A and B, and calculate the magnitude of the pushing or pulling force of each of the five bars on its end points, distinguishing which are pulls and which pushes.
By symmetry the reactive forces at A and B are equal, of magnitude R kg wt say.
The vector sum of all the external forces on the structure as a whole must be zero:

Hence each reactive force has magnitude

Now suppose the bars AC, AD and CD exert pushing forces of magnitude |x|, |y| and |z| kg wt respectively at their ends. Some of x, y, z may be negative, which will mean the corresponding bar pulls instead of pushes.
By symmetry BC and BD push with forces of magnitude |x| and |y| kg wt respectively.
Let 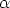 ,
, 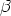 be the angles CAB, DAB respectively.
be the angles CAB, DAB respectively.
Clearly 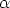 = tan -1
= tan -1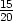 = tan -1
= tan -1 , and
, and 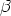 = tan -1
= tan -1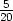 = tan -1
= tan -1 .
.
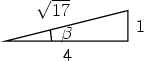
The forces at A sum to zero:

Equating i and j components gives two equations:

These have the unique solution
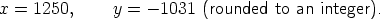
By symmetry, considering the forces at B gives equations (1) and (2) again.
Considering forces at C:

which gives one non-trivial equation:

which, using the value of x found above, gives

The forces at D give

which also yields one non-trivial equation:

This is satisfied by the values of y and z found above (and, indeed, equation (4) can be deduced from (2) and (3) by taking (3) - 2 × (2).)
So bars AC and BC push with a force of magnitude 1250 kg wt;
bars AD and BD pull with a force of magnitude approximately 1031 kg wt;
and bar CD pulls with a force of magnitude 500 kg wt.
Note: It is important to engineers which are pulls and which pushes -- chains can pull but not push, whereas concrete pylons can push, but would come apart if pulled.
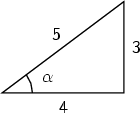
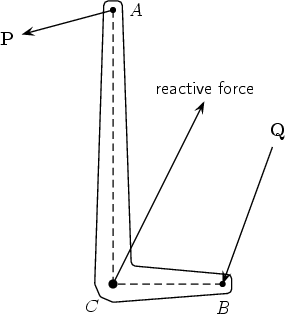
A bent lever has perpendicular arms CA (vertical, of length 30cm) and CB (horizontal, of length 12cm), and is pivoted at C. A force P of 35kg wt is applied at A at 15° to the horizontal, and another force Q is applied at B at 20° to the vertical, as shown in the diagram.
Assuming the situation is static, find the magnitude of Q, and the magnitude and direction of the reaction at C.
The magnitude of Q, can be determined from the fact that, because the situation is static, the sum of the moments of P and Q about C is zero:

i.e.,
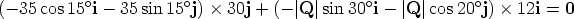
or

which gives

to 2 significant figures.
From the fact that the situation is static the reaction force at C must be the negative of the sum of the forces P and Q, that is,
| - P - Q | |||
| = | (35 cos 15°i + 35 sin 15°j) + (|Q| sin 20°i + |Q| cos 20°j) | ||
| = | 64.57i + 93.58j | ||
| = | 113.6(cos 55.4°i + sin 55.4°j). |