Advanced examples for Division of a line segment

Example 1

To illustrate the use of the formula for the division of a line segment in a certain ratio, consider the problem from classical geometry on the concurrency of the three medians of a triangle. Let ABC be any triangle, and let D, E and F be the midpoints of the three sides of the triangle, as shown in the diagram below. The three medians are AD, BE, and CF, and the problem is to prove first that they are concurrent (that is, if G is the point of intersection of AD and BE, then CF also passes through G), and then that the point G divides each median in the ratio 2 : 1.

Solution

Let the position vectors of A, B, C, D, E, F and G relative to some origin O be a, b, c, d, e, f and g respectively. For simplicity, the origin O and the seven position vectors are not drawn on the diagram. The formula for the position vector of the midpoint of a line segment then allows us to write

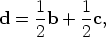
d = 1b + 1c, 2 2

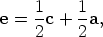
e = 1c + 1-a, 2 2

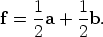
1 1 f = -a + --b. 2 2

Since G is defined to be the point of intersection of AD and BE, we seek an equation involving a, b, d, and e. This can be obtained by eliminating c from the first two equations above.

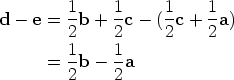
d - e = 1b + 1c - (1c + 1a) 2 2 2 2 1- 1- = 2b - 2a

After multiplying by 2, rearranging and dividing by 3, we obtain

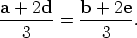
a-+-2d- b-+--2e 3 = 3 .

Now compare these expressions with the formula for the position vector (relative to O) of a point R on the line segment P₁P₂,

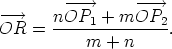
----> ----> ---> nOP1--+-m-OP2-- OR = m + n .

It is clear that 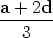a-+-2d- 3 is the position vector of a point on AD, and 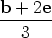b-+--2e 3 is a position vector of a point on BE. Since G is the point of intersection of these two lines, we see that

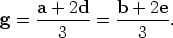
g = a +-2d-= b-+-2e. 3 3

These equations also show that G divides both AD and BE in the ratio 2 : 1.

Finally, to show that CF also passes through G, observe that

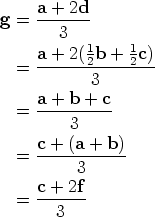
a-+-2d- g = 3 1 1 = a-+-2(2b-+--2c) 3 a-+-b-+-c- = 3 c + (a + b) = ------------ 3 = c-+-2f- 3

This shows that G lies on CF and divides CF in the ratio 2 : 1, as required.