
Quiz 9
 |
Quiz 9 |
|||||
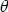 , where
, where 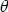 is the angle between the vectors when
placed tail to tail, we have
is the angle between the vectors when
placed tail to tail, we have  .
.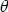 . The answer is 4.2.
. The answer is 4.2.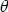 is the required angle, then cos
is the required angle, then cos 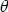 =
=  =
=  and hence
and hence  radians.
radians.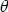 is the required angle, then cos
is the required angle, then cos 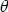 =
=  =
= 
 . Hence
. Hence

