The University of Sydney - School of Mathematics and Statistics

The vector product in terms of magnitudes, angles and the “right-hand rule”	Page 1 of 7

The vector product is a product of two vectors in space. The result of the multiplication is a vector, hence the name vector product. Other names for the vector product are cross product or outer product.

If u and v are vectors, their vector product is denoted by u × v. We must assign that product a direction and a magnitude.

We start by specifying the direction. Suppose that u and v are two non-zero and non-parallel vectors in space. When placed tail-to-tail they define a plane. There are two possibilities to choose a unit vector perpendicular to that plane: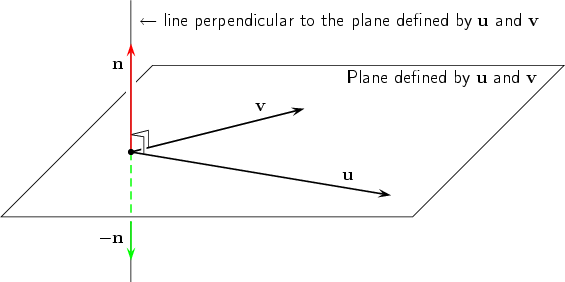

We choose n such that the triple u,v,n is right-handed. By this we mean the following. Align a screw-driver along the line perpendicular to the plane defined by u and v. Then turn the screw-driver such that u moves to v through the smaller angle. The direction of n is then given by the direction the screw moves.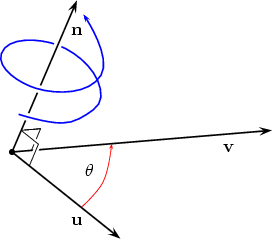

Note that it is irrelevant which way we align the screw-driver, the direction in which the screw moves will be the same either way.

Having established the direction it remains to define the magnitude of the vector product. We let the magnitude be |u||v| sin , where is the smaller angle between u and v.

Then we define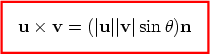

If u and v are parallel or one (or both) of them are zero vectors then we set u×v = 0. Geometrically, the magnitude equals the area of the parallelogram spanned by the vectors u and v when placed tail-to-tail.

Important Note: Unlike in the definition of the scalar product it is essential that the angle between u to v is the smaller one, that is, the one between 0° and 180°.