 |
||||||||||||||||||||||||||||||||||||||||||
|
3. Addition and subtraction of vectors
|
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Another way to define addition of two vectors is by a head-to-tail construction that creates two sides of a triangle. The third side of the triangle determines the sum of the two vectors, as shown below. Place the tail of the vector v at the head of the vector u. That is, u = 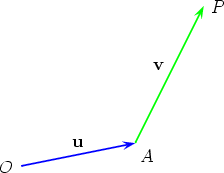
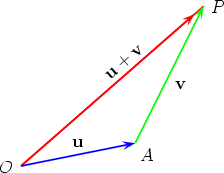
Now construct the vector 
This method is equivalent to the parallelogram law of addition, as can be easily seen by drawing a copy of v tail-to-tail with u, to obtain the same parallelogram as before. 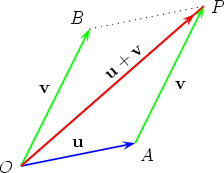
Using position vector notation, the triangle rule of addition is written as follows: for any three points X, Y , Z, 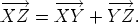 Both the triangle and the parallelogram rules of addition are procedures that are independent of the order of the vectors; that is, using either rule, it is always true that u + v = v + u for all vectors u and v. This is known as the commutative law of addition. There are other rules like this one, and they are discussed in the component Vector Algebra.
|
|||||||||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
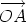 and
and
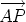 .
. 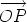 to complete the third side of the triangle
to complete the third side of the triangle