 |
||||||||||||||||||||||||||||||
|
6. Cartesian and polar coordinates in two dimensions
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
If you are looking at an aeroplane on a radar screen you could determine its position by giving its distance from you and a direction or angle, say northwest. Let us see how to do this in terms of coordinates. Imagine that the point Q represents the position of the aeroplane, and you are at the origin. 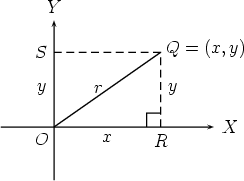
The length r of the line segment OQ is calculated by applying Pythagoras’ theorem to the right angled triangle ORQ. This gives  This formula for r is valid for both positive and negative values of x and y. To measure an angle or direction for Q we have to measure it starting from
somewhere. By convention, all angles are measured starting from the positive OX
axis, increasing in the anti-clockwise direction. Now we have the following
diagram, in which 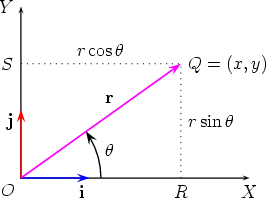
Elementary trigonometry and a comparison with the previous diagram show that 
where r is the length of OQ and 
Thus given the polar coordinates (r, 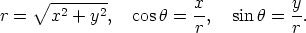
The actual value of As r = 
|
|||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
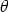
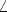
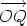 .
.

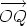
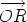
 , we obtain what is known as the
, we obtain what is known as the