School of Mathematics and Statistics, The University of Sydney
 7. Cartesian coordinates in three dimensions
Main menu Section menu   Previous section Next section Addition and subtraction of vectors in terms of components button disabled
Glossary
Assumed knowledge
Related topics
Examples

Multiplication by scalars in terms of components

Page 5 of 5 

If a vector is expressed in Cartesian form, then it’s easy to calculate any scalar multiple of that vector in Cartesian form.

The general rule is that given any vector v = xi + yj + zk and any scalar a, then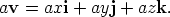

av = axi + ayj + azk.

For example, if v = 2i + j - k, then -4v = -8i - 4j + 4k.

The same formula applies in two dimensions. The vector v = xi + yj can be thought of as v = xi + yj + 0k. Then if a is any scalar,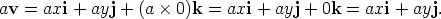

av = axi + ayj + (a × 0)k = axi + ayj + 0k = axi + ayj.

Thus if u = 2i + j then 2u = 4i + 2j, as illustrated in the following picture.

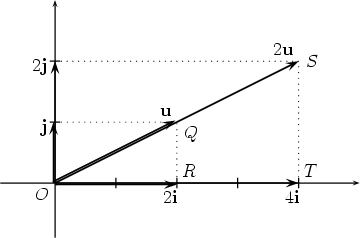
2j 2u S u j Q R T O 2i 4i

Feedback
Main menu Section menu   Previous section Next section Addition and subtraction of vectors in terms of components button disabled