JARCS 2005
Australian-Japanese Real and Complex Singularities
Workshop
Last updated: August 22, 2005
Back to Conference Home Page
List of Talks
Abstracts
1 E.N. Dancer (Sydney University, Australia): Removability of zeros and related
questions
Abstract: We discuss results and open problems on the removability of zeros of maps and of critical
points of scalar functions under small perturbations. Here what sort of perturbations we allow and what
we mean by small can sometimes affect the answer. We also discuss the problem for mappings with
symmetries.
In addition, we discuss some related problems on the existence of continua of solutions when we
perturb maps.
Back to top
2 T.-C. Kuo (Sydney University, Australia): Relative Newton Polygon, Local Algebraic Geometry
as Global Infinitesimal Calculus
Abstract: The Newton Polygon is a powerful tool for analytic singularities. It yields the
fundamental theorem of Newton-Puiseux. This lecture is an elementary exposé on this. For an
analytic function germ (convergent power series) f(x,y) and an analytic arc  , the Newton
Polygon of f relative to
, the Newton
Polygon of f relative to  , NP(f,
, NP(f, ) is defined. A number of important applications are
illustrated.
) is defined. A number of important applications are
illustrated.
Two seemingly unrelated problems are intimately connected.
The first is the equsingularity problem in R2: For an analytic family ft : (R2,0)  (R,0), when
should it be called an equisingular deformation? This amounts to finding a suitable trivialization
condition (as strong as possible) and, of course, a criterion.
(R,0), when
should it be called an equisingular deformation? This amounts to finding a suitable trivialization
condition (as strong as possible) and, of course, a criterion.
The second is on the Morse stability. We define R*, which is R “enriched” with a class of
infinitesimals. How to generalize the Morse Stability Theorem to polynomials over R*?
The space R* is much smaller than the space used in Non-standard Analysis. Our infinitesimals are
analytic arcs, represented by fractional power series, e.g., x = y3 + 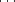 , x = y5/2 +
, x = y5/2 + 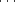 , x = y3/2 +
, x = y3/2 + 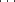 ,
are infinitesimals at 0
,
are infinitesimals at 0  R, in descending orders.
R, in descending orders.
Thus, pt(x):= ft(x,y):= x4 - t2x2y2 - y4 is a family of polynomials over R*. This family is not
Morse stable: a triple critical point in R* splits into three when t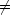 0.
0.
Back to top
3 Amnon Neeman (Australian National University, Australia): The derived categories of
singularities as compactly generated triangulated categories
Abstract: The talk will begin with a survey of the theory of compactly generated triangulated
categories. We will explain the history and the many applications that have been found. The link with
singularity theory is a recent result by Henning Krause, which exhibits the derived category of a
singularity, in the sense of Kontsevich, as the compact objects in an infinite derived category. This
immediately raises interesting questions, for example whether there is an infinite version of the Fukaya
category, and an infinite version of mirror symmetry.
Back to top
4 Mike Eastwood (Adelaide University, Australia): Moduli of isolated hypersurface
singularities
Abstract: John Mather and Stephen Yau showed that isolated singularities of complex hypersurfaces
are classified by their associated deformation algebras. This suggests that one should be able to associate
invariants to a hypersurface singularity via its deformation algebra. I shall explain how this can be
done.
Back to top
5 Paul Norbury (University of Melbourne, Australia): Topological invariants of complex curve
singularities
Abstract:
A complex curve singularity can be viewed as a complex codimension 1 condition on a family of
curves - count the number of times the singularity appears on curves in the family - and thus a
second cohomology class in the compactified moduli space Mg,n of genus g curves with n
marked points. A polynomial in two complex variables p : C2  C plays a dual role. It gives a
second homology class in Mg,n consisting of the complex 1 dimensional family of curves
p(x,y) = c as c varies, where the marked points are the points at infinity on each curve. The
cohomology and homology classes give topological information about the singularity and
polynomial.
C plays a dual role. It gives a
second homology class in Mg,n consisting of the complex 1 dimensional family of curves
p(x,y) = c as c varies, where the marked points are the points at infinity on each curve. The
cohomology and homology classes give topological information about the singularity and
polynomial.
Complex plane curve singularities can be studied using the link of the singularity, a topological
invariant which is a link in the 3-sphere obtained by intersecting the curve with the boundary of a very
small ball around the singularity. Similarly, a topological invariant given by a link in the 3-sphere
can be associated to a polynomial in two complex variables as the intersection of a generic
curve in the family p(x,y) = c with the boundary of a very large ball. It is known as the
link at infinity of the polynomial. The link at infinity yields other topological information
about the polynomial, such as the genus of the generic curve in the family, the monodromy
around non-generic curves in the family, and possible non-generic curves that can arise in the
family.
This lecture will address the question of how much the link at infinity can say about the second
homology class in Mg,n. Most of the lecture will be an introduction to the different ingredients involved
in the construction of these topological invariants.
Back to top
6 Kiyoshi Takeuchi (Tsukuba University, Japan): Projective duality and topological Radon
transforms (joint work with Y. Matsui)
Abstract: It is well-known that inflection points of an algebraic curve correspond to cusps of the dual
curve. This basic correspondence (projective duality) has various generalizations in higher-dimensional
cases. In this talk we shall give such results using topological Radon transforms of subanalytically
constructible functions. Microlocal theory of sheaves developed by Kashiwara-Schapira will be used in
the proofs. We also give a formula for the degrees of associated hypersurfaces studied by
Gelfand-Kapranov-Zelevinski.
Back to top
7 Takuo Fukuda (Nihon University, Japan): Smooth integrability of implicit differental systems
(joint work with S. Janeczko)
Abstract: Takuo Fukuda Smooth int4egrability of implicit differential systems ( joint work with S.
Janeczko)
We regard a smooth submanifold M of the tangent bundle TRn as a differential equation and call it
an implicit differential system. A solution of such an implicit differential system M is a curve
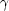 : (a,b)
: (a,b)  Rn such that (
Rn such that (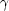 (t),
(t),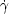 (t))
(t))  M for all t
M for all t  (a,b). A point (x0,
(a,b). A point (x0,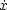 0)
0)  M is an integrable point of
M if there exists a solution
M is an integrable point of
M if there exists a solution 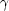 : (a,b)
: (a,b)  Rn of the implicit differential system M such that
(
Rn of the implicit differential system M such that
(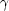 (0),
(0),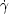 (0)) = (x0,
(0)) = (x0,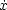 0) for 0
0) for 0  (a,b). (x0,
(a,b). (x0,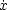 0)
0)  M is a smoothly integrable point of M if there exist a
neighborhood U of (x0,
M is a smoothly integrable point of M if there exist a
neighborhood U of (x0,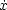 0) in M and a family {
0) in M and a family {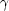 (x,
(x, ) | (x,
) | (x,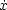 )
)  U} of solutions of M staisfying the initial
condition (
U} of solutions of M staisfying the initial
condition (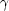 (x,
(x, )(0),
)(0),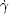 (0)) = (x,
(0)) = (x,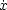 ) which depends smoothly on (x,
) which depends smoothly on (x,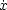 )
)  U. The differential system M is
smoothly integrable if every point (x0,
U. The differential system M is
smoothly integrable if every point (x0,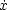 0)
0)  M is inetegrable. We investigate when these implicit
differential systems are smoothly integrable.
M is inetegrable. We investigate when these implicit
differential systems are smoothly integrable.
Next we consider a Lagrangian submanifold L 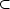 TR2n as an implicit differential system,
here TR2n is a symplectic manifold with the following natural symplectic structure
TR2n as an implicit differential system,
here TR2n is a symplectic manifold with the following natural symplectic structure  . Let
(x,y) = (x1,cdots,xn,y1,
. Let
(x,y) = (x1,cdots,xn,y1,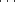 ,yn) be the stanndard coodinates and let
,yn) be the stanndard coodinates and let  =
= 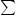 i=1ndyi
i=1ndyi  dxi be the
canonical symplectic structure on R2n. Then bar
dxi be the
canonical symplectic structure on R2n. Then bar =
= 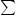 i=1nd
i=1nd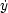 i
i  dxi - d
dxi - d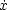 i
i  dyi is the natural
symplectic structure on TR2n which is derived from the one on T*R2n. We regard Lagrangian
submanifolds of the symplectic manifold TR2n as implicit differential systems and call them
implicit Hamiltonian systems. The necessity for studing such implicit Hamiltonian systems was
first suggested by P.A.M. Dirac in Quantum Field Theory at the begining of 1950’s. We
study local and global properties of solutions of smoothly integrable implicit Hamiltonian
systems.
Back to top
dyi is the natural
symplectic structure on TR2n which is derived from the one on T*R2n. We regard Lagrangian
submanifolds of the symplectic manifold TR2n as implicit differential systems and call them
implicit Hamiltonian systems. The necessity for studing such implicit Hamiltonian systems was
first suggested by P.A.M. Dirac in Quantum Field Theory at the begining of 1950’s. We
study local and global properties of solutions of smoothly integrable implicit Hamiltonian
systems.
Back to top
8 Mariko Ohsumi (Nihon University, Japan): Whitney’s umbrellas in stable perturbations
of a map germ (Rn,0)  (R2n-1,0)
(R2n-1,0)
Abstract: In this talk we show that the number modulo 2 of Whitney’s umbrellas that appear in
stable perturbations of a generic C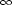 map-germ f : (Rn,0)
map-germ f : (Rn,0)  (R2n-1,0) is a topological
invariants.
(R2n-1,0) is a topological
invariants.
Let f : (Rn,0)  (R2n-1,0) be a C
(R2n-1,0) be a C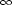 map-germ and let
map-germ and let 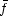 : U
: U  R2n-1 be a C
R2n-1 be a C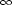 representive of f, U
being a small open neighborhood of the origin 0 in Rn. By Whitney’s theorem,
representive of f, U
being a small open neighborhood of the origin 0 in Rn. By Whitney’s theorem, 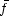 can be approximated
by a stable mapping
can be approximated
by a stable mapping 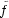 : U
: U  R2n-1 whose singularities are only Whitney’s umbrellas. We call such
R2n-1 whose singularities are only Whitney’s umbrellas. We call such
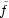 : U
: U  R2n-1 a stable perturbation of f : (Rn,0)
R2n-1 a stable perturbation of f : (Rn,0)  (R2n-1,0).
(R2n-1,0).
We are interested in the number of Whitney’s umbrellas of 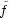 .
.
Let En be the ring of C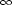 function-germs of (Rn,0) into R. Let f : (Rn,0)
function-germs of (Rn,0) into R. Let f : (Rn,0)  (R2n-1,0) be a C
(R2n-1,0) be a C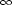 map-germ. Let I(
map-germ. Let I(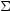 1(f)) be the ideal in En generated by n × n mirnor determinants of the jacobian
matrix of f.
1(f)) be the ideal in En generated by n × n mirnor determinants of the jacobian
matrix of f.
Main theorem. Let f : (Rn,0)  (R2n-1,0) be a generic C
(R2n-1,0) be a generic C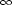 map-germ such that
dimREn/I(
map-germ such that
dimREn/I(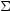 1(f)) < +
1(f)) < +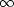 . The number of Whitney’s umbrellas that appear in a stable perturbation
. The number of Whitney’s umbrellas that appear in a stable perturbation 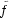 of f
is equal to dimREn/I(
of f
is equal to dimREn/I(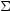 1(f)) (modulo 2) and it is a topological invariant of f.
1(f)) (modulo 2) and it is a topological invariant of f.
The statement that the number is equal to dimREn/I(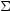 1(f)) (mod 2) is already known. Our
assertion in the above theorem is that it is a topological invariant of f.
Back to top
1(f)) (mod 2) is already known. Our
assertion in the above theorem is that it is a topological invariant of f.
Back to top
9 Shuzo Izumi (Kinki University, Japan): Fundamental properties of analytic mappings between
germs of analytic sets
Abstract: Let 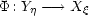 be a germ of an analytic map of analytic sets irreducible at
be a germ of an analytic map of analytic sets irreducible at 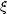 and
and 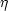 respectively. It induces a homomorphism
respectively. It induces a homomorphism 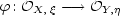 of local integral domains by pullback:
of local integral domains by pullback:
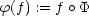 . Let
. Let 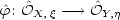 be the canonically induced homomorphism, the completion of
be the canonically induced homomorphism, the completion of 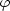 .
Let us put:
.
Let us put:
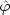 (formal rank, the Krull dimension of the formal closure of the image of
(formal rank, the Krull dimension of the formal closure of the image of 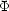 )
)
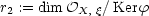 (analytic rank, the Krull dimension of the analytic closure of the
image of
(analytic rank, the Krull dimension of the analytic closure of the
image of 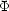 )
)
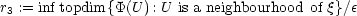 (topological rank,
(topological rank,  = 2 in complex
case, = 1 in real case)
= 2 in complex
case, = 1 in real case)
It is known that r1 < r2 < r3. (The first inequality is not trivial.) Let 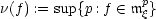 denote the (algebraic) order of
denote the (algebraic) order of 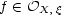 .
.
Then the condition r1 = r2 = r3 is equivalent to each of the following:
- r1 = r2 in complex case (Gabrielov 1973; cf. Tougeron 1990, Hübl 2001).
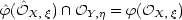 (Gabrielov 1973; cf. I. 1989, Tougeron 1990, Hübl 2001).
(Gabrielov 1973; cf. I. 1989, Tougeron 1990, Hübl 2001).
- The image of
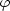 is closed with respect to Krull topology (Becker-Zame 1979; cf. I. 1989).
is closed with respect to Krull topology (Becker-Zame 1979; cf. I. 1989).
- The image of
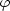 is closed in
is closed in 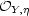 and open in the image with respect to Krull topology
(Gabrielov 1973; cf. Becker-Zame 1979, I. 1989).
and open in the image with respect to Krull topology
(Gabrielov 1973; cf. Becker-Zame 1979, I. 1989).
- There are constants a > 1 and b > 0 such that, for
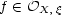 , there exists
, there exists 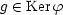 such
that
such
that 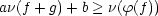 (I. 1985, 1986).
(I. 1985, 1986).
Back to top
10 Kimio Miyajima (Kagoshima University, Japan): Deformation of CR structure on a link of
isolated singularities
Abstract: The versal deformation and its construction is one of main interests of moduli problem. After
K. Kodaira and D. C. Spencer constructed the versal family of compact complex manifolds, various
method were developed. Although the PDE-method was useful for application of moduli theory to wide
range of mathematics, it is not fully developed for the moduli of singular variety. In this talk, I would like
to talk about the M. Kuranishi’s problem on the PDE-construction of the versal deformation of normal
isolated singularities; Construct the versal deformation of normal isolated singularity germ by means of
CR sturucture on its link. I would like to give an overview of this problem, its solution and some related
topics.
Back to top
11 Shyuichi Izumiya (Hokkaido University, Japan): Singularity theory of smooth mappings and
its applications -expository talk to non-specialists
Abstract: This is an expository talk on singularity theory of smooth mappings and its applications. It
contains the following topics:
- Singularities of smooth functions.
- Whitney’s classical theory on smooth mapping.
- Differential geometry and shapes of surfaces.
- Singularities of solutions for first order PDE.
- Other topics.
Back to top
12 Goo Ishikawa (Hokkaido University, Japan): Singularities of parametric plane curves and
Legendre curves
Abstract: The classification problem of parametric plane curve singularities is closely related to that of
Legendre curve singulariteis in the contact three space and Goursat flags in the theory of differential
systems. We provide the recent result on the complex symplectic moduli space of simple and uni-modal
plane curve singulariites and discuss its relation to the contactomorphism classification of Legendre curve
singularities.
Back to top
13 Kazuhiro Sakuma (Kinki University, Japan): The existence of fold maps into
R3
Abstract: Let Mn be a closed n-manifold and f : Mn  Rp a smooth map, provided that n > p. If f
has only fold singularities as its singularities, then f is called a fold map. When p = 1, a fold map is
nothing but a Morse function. Then we will consider a problem belonging to global singularity theory:
Find the necessary and/or sufficient condition(s) for the existence of fold maps. When p = 3,7 relating to
the parity of the Euler characteristic of the source manifold, the existence of fold maps has a special
position in the problem. We will discuss the problem on the case that p = 3,7 separately by summarizing
recent results in relation with the Thom polynomials, the Elishberg-Ando h-principle theorem, etc.
Moreover, when n is even, we can conclude that the case only for (n,p) = (4,3) in the problem is
exceptional by combining Sadykov’s theorem with four dimensional topology. We will also give the
sufficient condition for the existence problem depending on the case that (n,p) = (4m + 1,3) or
(4m + 3,3).
Rp a smooth map, provided that n > p. If f
has only fold singularities as its singularities, then f is called a fold map. When p = 1, a fold map is
nothing but a Morse function. Then we will consider a problem belonging to global singularity theory:
Find the necessary and/or sufficient condition(s) for the existence of fold maps. When p = 3,7 relating to
the parity of the Euler characteristic of the source manifold, the existence of fold maps has a special
position in the problem. We will discuss the problem on the case that p = 3,7 separately by summarizing
recent results in relation with the Thom polynomials, the Elishberg-Ando h-principle theorem, etc.
Moreover, when n is even, we can conclude that the case only for (n,p) = (4,3) in the problem is
exceptional by combining Sadykov’s theorem with four dimensional topology. We will also give the
sufficient condition for the existence problem depending on the case that (n,p) = (4m + 1,3) or
(4m + 3,3).
Back to top
14 Masatomo Takahashi (Hokkaido University, Japan): Second order ordinary differentical
equations of Clairaut type
Abstract:
I am going to talk about on implicit second order ordinary differential equations with complete
integral. In paticular, we consider equation has a smooth complete solution, namely, it is parameterized
by two parameter family of classical solutions. On the other hand, we consider second order Clairaut
type equations. It is one of generalization of the notion of second order classical Clairaut equations like as
first order cases. We give a characterization of smooth completely integarble and second order Clairaut
type. Moreover, we give generic classifications of Clairaut type equations by certain equivalence
relations.
Back to top
15 Jiro Adachi (Hokkaido University, Japan): On horizontal loops in the standard Engel
space
Abstract:
Engel structure is one of rare geometric structures on a manifold which are locally stable, like
contact structure. Like Legendrian knot theory for contact topology, horizontal loops for Engel
structures might be important objects to consider. I would like to introduce the classification
of horizontal loops in the standard Engel space, first, from the view point of Legendrian
knot theory with singularities. Further, I would like to consider it from the view point of
h-principle.
Back to top
16 Takahiro Yamamoto (Hokkaido University, Japan): The singular fibers of generic maps and
Surface bundles
Abstract: In this talk, we consider the characterization of the topology of Surface bundles  : E
: E  B
by the generic functions f : E
B
by the generic functions f : E  R on the total spaces. In this situation, we consider the set of
points q in B for which the restriction of f to the fiber over q (we denote it by fq) is not a
stable Morse function. On the other hand, we characterize the smooth functions on surfaces
by the inverse image germs of degenerate critical values. Then, we obtain representation of
characteristic classes by the set of points q whose corresponding fq has certain type inverse image
germ.
R on the total spaces. In this situation, we consider the set of
points q in B for which the restriction of f to the fiber over q (we denote it by fq) is not a
stable Morse function. On the other hand, we characterize the smooth functions on surfaces
by the inverse image germs of degenerate critical values. Then, we obtain representation of
characteristic classes by the set of points q whose corresponding fq has certain type inverse image
germ.
Back to top
Page maintained by Laurentiu Paunescu, School of Mathematics and Statistics, The University of
Sydney
 (R2n-1,0)
(R2n-1,0)

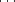 ,
, 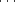 ,
, 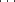 ,
are infinitesimals at 0
,
are infinitesimals at 0 
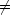 0.
0.
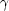
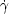 (
(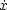
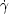 (0)) = (
(0)) = (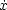
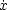
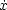

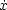 )
) 
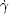 (0)) = (
(0)) = (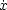 ) which depends smoothly on (
) which depends smoothly on (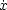 )
) 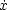
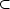
 . Let
(
. Let
(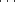

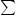

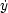
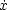
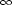
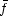 :
: 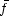 can be approximated
by a stable mapping
can be approximated
by a stable mapping 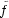 :
: 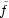 :
: 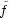 .
.
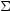
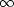
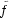
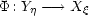 be a germ of an analytic map of analytic sets irreducible at
be a germ of an analytic map of analytic sets irreducible at 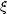
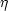
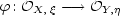 of local integral domains by pullback:
of local integral domains by pullback:
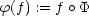 . Let
. Let 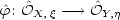 be the canonically induced homomorphism, the
be the canonically induced homomorphism, the 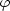
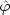 (
(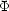 )
)
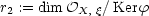 (
(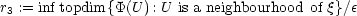 (
(
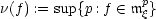 denote the
denote the 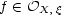 .
.
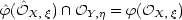 (Gabrielov 1973; cf. I. 1989, Tougeron 1990, Hübl 2001).
(Gabrielov 1973; cf. I. 1989, Tougeron 1990, Hübl 2001).
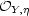 and open in the image with respect to Krull topology
(Gabrielov 1973; cf. Becker-Zame 1979, I. 1989).
and open in the image with respect to Krull topology
(Gabrielov 1973; cf. Becker-Zame 1979, I. 1989).
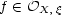 , there exists
, there exists 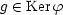 such
that
such
that 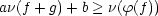 (I. 1985, 1986).
(I. 1985, 1986).