Joel Gibson
I am a recent postgraduate of the School of Mathematics at Sydney University. I recevied my PhD in 2020, under the guidance of Oded Yacobi. For my contact details and teaching timetable, see my people page on the School of Maths system.
Seminars
I created the Student Algebra Seminar and ran it for four semesters. As of Semester 2, 2020 it is run by Joshua Ciappara. The sessions I organised are below:
In Semester 2 of 2018, I coordinated a reading group on the Geometric Satake correspondence.
My work
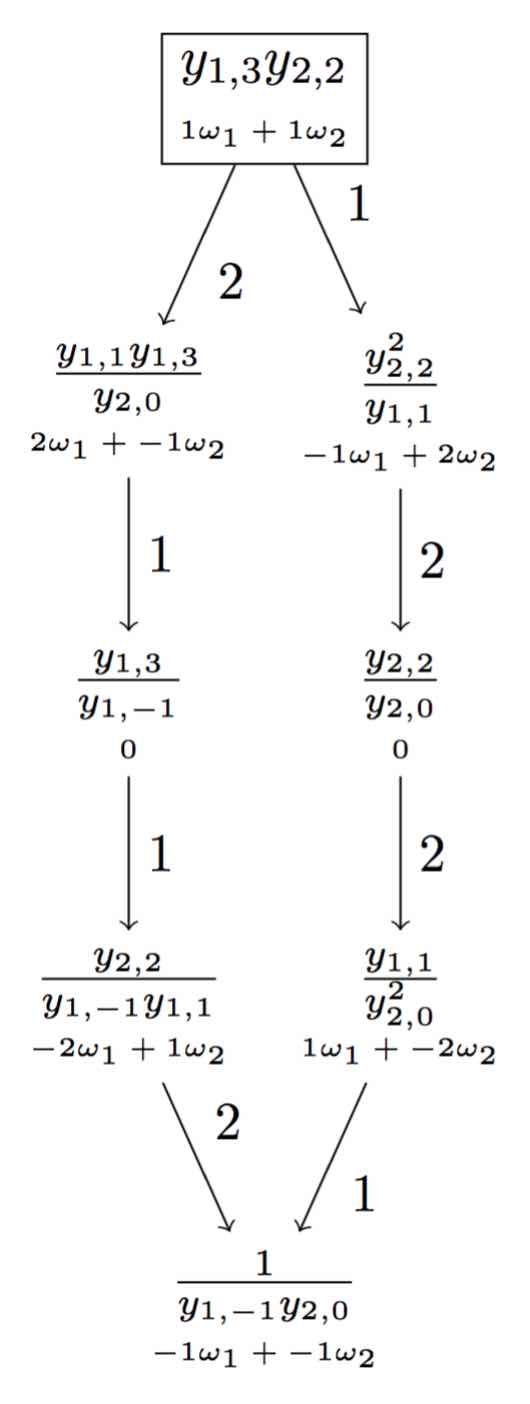
I have a long-term project investigating the structure of the "product monomial crystal" in Type A. The product monomial crystal is defined in the paper Highest weights for truncated shifted Yangians and product monomial crystals, and is a subcrystal of Nakajima's crystal of monomials for any semisimple simply-laced Lie algebra, formed by the monomial-wise multiplcation of various fundamental crystals. The image on the right shows one realisation of the crystal of the sl3 adjoint representation, as a product monomial crystal.
The product monomial crystal depends on its input parameters in a rather mysterious way, interpolating between a tensor product of fundamental crystals, and the irreducible with highest weight being the sum of those fundamentals. To assist in various computations, I created a program which can compute this crystal for any input data, and list its decomposition into irreducible components. There are instructions for how to download and run the program.
The character of the product monomial crystal for any simply-laced type can be computed in terms of Demazure operators, and multiplications by fundamental weights. In type A, the product monomial crystal is the crystal of a generalised Schur module, a generalisation of both irreducible modules and skew-Schur modules. This research is available in a preprint: arXiv:1907.09681 [math.CO], and also in my thesis.
Talks
- I gave a talk on the product monomial crystal at AustMS 2018, held at the University of Adelaide, which was one of the two winners of the Bernhard Neumann prize for most outstanding student talk. Here are both the slides and annotated slides for the talk. (To view the annotated slides, open your PDF reader in "two pages per screen" mode).
Posters
- A poster on a conjecture (now a theorem) on the representation afforded by a graded Nakajima quiver variety. This was presented at the Future Directions in Representation Theory conference held at the University of Sydney in 2017. PDF
- A poster explaining a problem in combinatorial commutative algebra to do with the embedding of the affine Grassmannian of SLn into the infinite (or Sato) Grassmannian. This was presented at the New Connections in Representation Theory conference held in Mooloolaba, Queensland in 2020. I experimented with making this poster in HTML rather than LaTeX and it turned out rather well – feel free to investigate the (a little messy) source code. HTML, PDF.
Other projects
Sometimes I write programs related to mathematics.
- A calculator for Littlewood-Richardson coefficients which runs in the browser. The code is simple (but not fast), relying on the combinatorics of GLn crystals to compute tensor product multiplicities.
- A calculator for Kronecker coefficients and more generally, character tables of the symmetric groups. For small symmetric groups (n ≤ 12 or so), it can compute tensor product multiplicities, as well as symmetric, alternating, and tensor powers of representations.
- I've been experimenting with making visualisations of rank 2 reductive groups, and in particular computing characters of representations in positive characteristic.