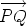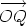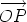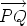|
||||||||||||||||||||||||||||||||||||||||||
|
14. Line Vectors
|
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
When a force acts on a body it can cause it to move in a particular direction and it can also cause it to twist. (Think of a spanner or wrench turning a bolt.) In order to measure the twist we introduce the concept of the moment of a line vector about a point. 
It doesn’t matter which point P on
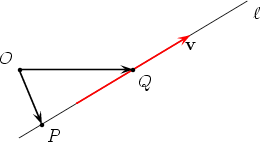
When calculating the moment of a line vector (
|
|||||||||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
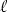
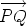 is parallel to
is parallel to