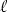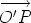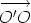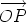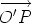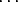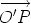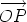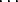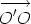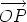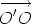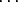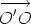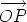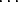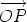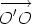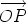The University of Sydney - School of Mathematics and Statistics

Systems of line vectors	Page 3 of 4

A collection of line vectors (₁,v₁), (₂,v₂), . . . , (_s,v_s) is also called a system of line vectors. The same line vector can occur more than once in the system but the order is not important.

The resultant of this system is the vector R that is the sum of all the individual vectors. That is,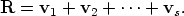

Suppose that O and O' are points. Let us compare the sum of the moments of the system of line vectors about the point O and about the point O'.

For each line _i choose a point P_i on _i. Then _i = + _i and so

1 × v1	+ + s × vs
	= ( + 1) × v1 + + ( + s) × vs
	= ( × v 1 + + × v s) + (1 × v1 + + s × vs)
	= × R + ( 1 × v1 + + s × vs)

We say that two systems of line vectors (₁,v₁), (₂,v₂), . . . , (_s,v_s) and (m₁,w₁), (m₂,w₂), . . . , (m_t,w_t) are equivalent if they have the same resultant and the same moment about any point O.

The calculation just carried out shows that this definition does not depend on the point O.

When we consider the behaviour of a rigid body under the action of a system of forces, equivalent systems of forces produce the same effect on the body: the same resultant “push” or “pull” and the same amount of “twist”.