Abstract
Starting point of this exposition is a construction of the Mercator map (see below) and its properties. We then show that the Mercator map is a limit case of a whole family of conformal (angle preserving) projections of the sphere onto the plane. The family is referred to as the Lambert conic conformal projections discovered by Lambert in 1772. We then show that the other limit case of this family is the stereographic projection. We also discuss some cases in between.
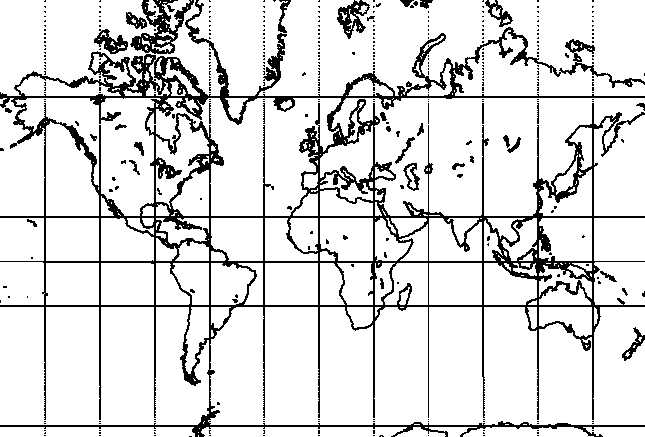
The exposition is aimed at everyone knowing elementary calculus. In particular it is accessible to high school and first year university students.
You can watch a movie (avi file) how the stereographic projection morphs from the stereographic projection from the south pole to the stereographic projection from the north pole via conic conformal maps. As a special case in the "middle" the Mercator projection appears.