Joanna Janczewska

Homoclinic solutions for a class of Hamiltonian systems”

We study the existence of homoclinic orbits for the second order Hamiltonian system 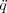+ V _q(t,q) = f(t), where q Rⁿ and V C¹(R × Rⁿ,R), V (t,q) = -K(t,q) + W(t,q) is T-periodic in t. A map K satisfies the ”pinching” condition b₁|q|² ≤ K(t,q) ≤ b₂|q|², W is superlinear at the infinity and f is sufficiently small in L²(R,Rⁿ). A homoclinic orbit is obtained as a limit of 2kT-periodic solutions of a certain sequence of the second order differential equations.